Influence Line

Influence Line:

Assume,

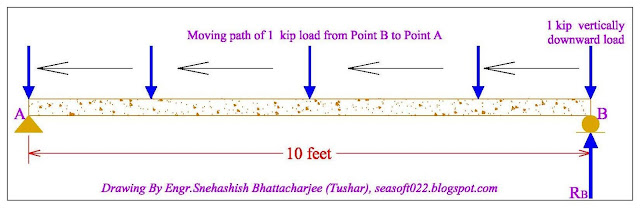
Here AB is a simply-support beam. 1 kip load is applied downward on the point A.We will get an upward reaction value (noted as R_A) at Point A because of applied 1 kip downward load.

Now when that 1 kip downward load is moved from Point A to Point B then this load (1 kip) will act all points on the beam AB & we will get a different reaction value of R_A each time while 1 kip load will move on the different points of beam AB (Point A to Point B). By adding these all reaction values of R_A, we will get a straight line. This straight line will known to us as Influence Line for R_A that is IL for R_A.

Now by the same way, we apply that 1 kip vertically downward load at Point B at first. We will get an upward reaction value (noted as R_B) at point B. Now move this load from Point B to Point A. We will get a different reaction value of R_B each time while 1 kip load will move on the different points of beam AB (Point B to Point A). By adding these all reaction values of R_B, we will get a straight line. This straight line will known to us as Influence Line for R_B that is IL for R_B.

Example-01:

Draw Influence Line for R_A and R_B.

Solution:

IL of R_A:

Now at first put 1 kip load downward at point A and then move this 1 kip load from Point A to Point B, we get,

When 1 kip load at first on the Point A then reaction of A that is R_A=1, RB=0, because total applied load is resisted by R_A.

Now when 1 kip is started to move from Point A to Point B and at last will rest on Point B then R_A=0 and R_B=1.

Now if we want to draw the influence line for R_A, then we get the following structure,

When 1 kip load rest upon Point A then R_A=1 and when 1 kip load rest upon Point B then R_A=0.

But as the definition of Influence Line, we need to add all reaction values which we will get from all points upon AB, during moving of 1 kip downward load from Point A to Point B. But here we have added reaction values only when 1 kip load rests at starting point and Ending Point.

Now we will calculate different reaction values of R_A from different points on beam AB.

At first consider the 1 kip load rests at Point C which is located at a distance 2 feet from point A.

Then,

∑M_A= 1*2 – R_B*10 = 0

So, R_B = 0.2 kip,

∑F_Y= R_A – 1 + 0.2 = 0

So, R_A= 0.8 kip.

Now consider the 1 kip load rests at Point D which is located at a distance 5 feet from point A.

Then,

∑M_A= 1*5 – R_B*10 = 0

So, R_B = 0.5 kip,

∑F_Y= R_A – 1 + 0.5 = 0

So, R_A= 0.5 kip.

Though 1 kip load is applied at middle point of AB then R_A will be half of applied load and R_B will be another half of applied load that means the summation of R_A & R_B will be the equal value of the applied load.

Now consider the 1 kip load rests at Point E which is located at a distance 8 feet from point A.

Then,

∑M_A= 1*8 – R_B*10 = 0

So, R_B = 0.8 kip,

∑F_Y= R_A – 1 + 0.5 = 0

So, R_A= 0.2 kip.

Now put all these reaction values of R_A and plot them on a Plain Graph Paper, which values we have already calculated by applying 1 kip load at Point C, D & E.

After plotting them on a Plain Graph Paper we get IL of R_A which is similar with the previous, by this experiment we can take decision that,

To find IL of any Simply Supported Beam we need to find only two reaction values at Starting Point & at Ending Point, we need not find any more reaction values at any other point on the BEAM.

IL for R_{B :}

When 1 kip load at first on the Point B then reaction of B that is R_B=1, R_A=0, because total applied load is resisted by R_B.

Now when 1 kip is started to move from Point B to Point A and at last will rest on Point A then R_B=0 and R_A=1.

So IL of R_B will be as follows,

We need not calculate different reaction values of R_B from different points on beam AB, because IL will be same (it is already proved for R_A)